1.总体流程
flowchart LR
A[输入原始图像] --> B[转化灰度图]
B -->C[计算非均匀权重掩膜]
C -->D[SMD梯度计算]
D --> E[Roberts算子灰度梯度计算]
E --> F[结束]
2.SMD-Roberts梯度模型
SMD原理
SMD(Sum of Modulus of Differences)函数是一种基于灰度梯度变化的图像清晰度评价算子,其基本思想是:当图像处于清晰状态时,相邻像素间的灰度变化幅度较大;而当图像发生模糊时,灰度变化趋于平缓,相邻像素间差值减小。因此,通过计算图像中相邻像素灰度差的总和,可以有效衡量图像的聚焦清晰程度。
SMD公式
$$
\begin{equation}
F_{\mathrm{SMD}} =
\sum_{x=1}^{M-1} \sum_{y=1}^{N-1}
\left(
\left| f(x+1, y) - f(x, y) \right| +
\left| f(x, y+1) - f(x, y) \right|
\right)
\label{eq:SMD_abs}
\end{equation}
$$
其中,\( f(x,y) \)表示图像在坐标\( (x,y) \)处的灰度值,\(N\)与\(M\)分别为图像的行列数。第一个差分项反映了图像在水平方向上的灰度变化,第二个差分项反映了垂直方向上的灰度变化,两者相加构成整体梯度能量。
Roberts公式
$$
\begin{equation}
F_{\mathrm{Roberts}}(x, y)
= \sqrt{\, G_x^2(x, y) + G_y^2(x, y) \,}
\label{eq:Roberts_mag}
\end{equation}
$$
SMD-Roberts融合公式
单点:
$$
\begin{equation}
F_{\mathrm{SMD\text{-}Roberts}}(x, y) =
\left( f(x+1, y) - f(x, y) \right)^2 +
\left( f(x, y+1) - f(x, y) \right)^2 +
\left( f(x+1, y+1) - f(x, y) \right)^2 +
\left( f(x+1, y-1) - f(x, y) \right)^2
\label{eq:SMD_Roberts_pixel}
\end{equation}
$$
全图:
$$
\begin{equation}
F_{\mathrm{SMD\text{-}Roberts}} =
\sum_{x=1}^{M-1} \sum_{y=1}^{N-1}
\Big[
\left( f(x+1, y) - f(x, y) \right)^2 +
\left( f(x, y+1) - f(x, y) \right)^2 +
\left( f(x+1, y+1) - f(x, y) \right)^2 +
\left( f(x+1, y-1) - f(x, y) \right)^2
\Big]
\label{eq:SMD_Roberts_total}
\end{equation}
$$
由于SMD只能计算水平和垂直方向的灰度梯度,融合Roberts则把±45°的梯度都加入考量可以提高鲁棒性。对原来公式取绝对值优化成取平方,可以有效提高高频信息,对边缘复杂的情况会有更好的判断。
3.非均匀权重掩膜
由于眼球部分存在睫毛、眼睑等组织影响最终判断,而我们需要的是Placido盘在虹膜上的清晰度,因此取一个非均匀权重掩膜来排除睫毛、眼睑等组织的影响。如下图1,取中心的权重较高,越往外部权重越小,符合眼睛的结构分布。

4.效果展示
在实验中发现由于镜头景深问题,Placido的虚像为目标图像,当Placido的虚像离焦时睫毛有可能在焦导致虚假的高评分。如下图2,3分别是没添加掩膜和添加了掩膜对同一组数据进行评分的结果。
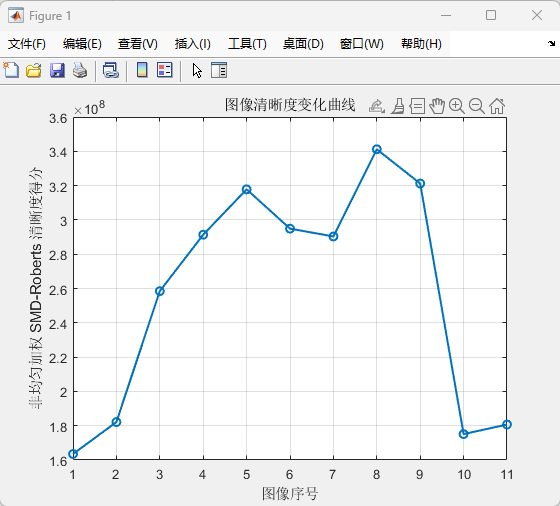
图2 未添加掩膜得分输出
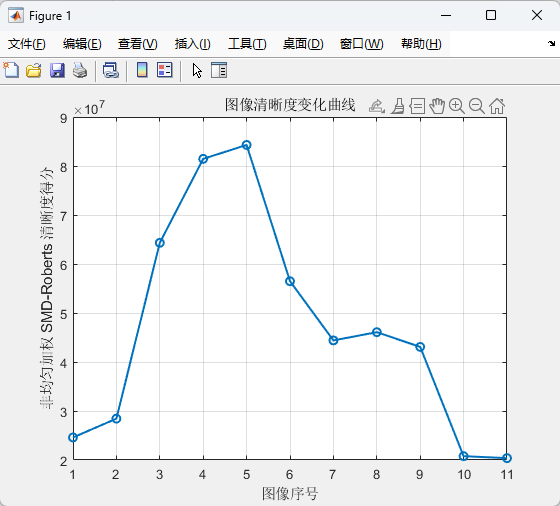
图3 添加掩膜后得分输出
从图中可以看出,未添加掩膜时序列号为5的图像和序列号为9的图像都得分都很高,实际上如下图4,5所示,序列号为9的图像是Placido虚像明显离焦的图像,得分高完全是因为眼睑和眼睫毛在焦导致被认为在焦,严重影响判断。因此根据先验知识加入掩膜,可以得到更加准确的评分系统。
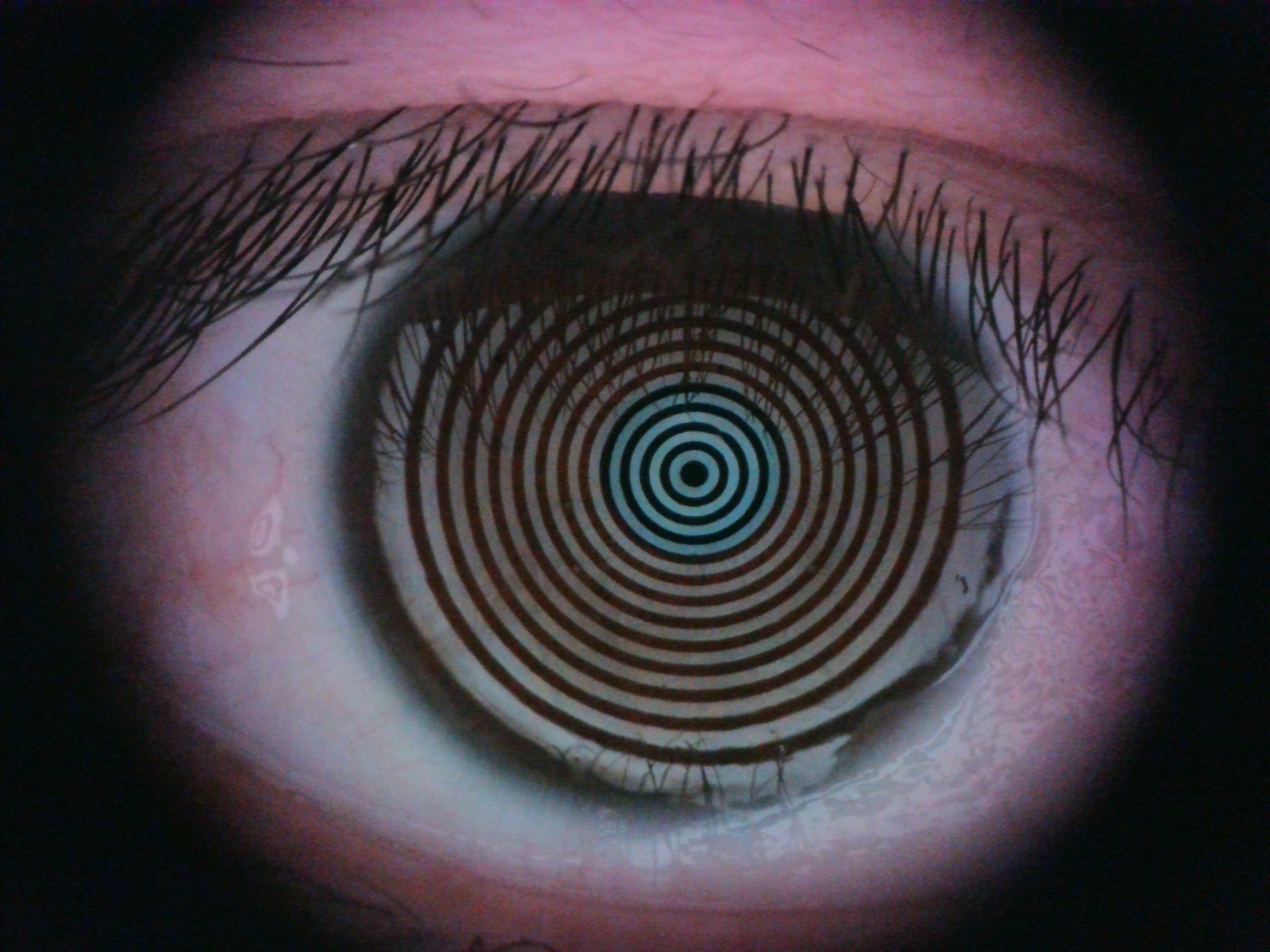
图4 序列号为5的图像
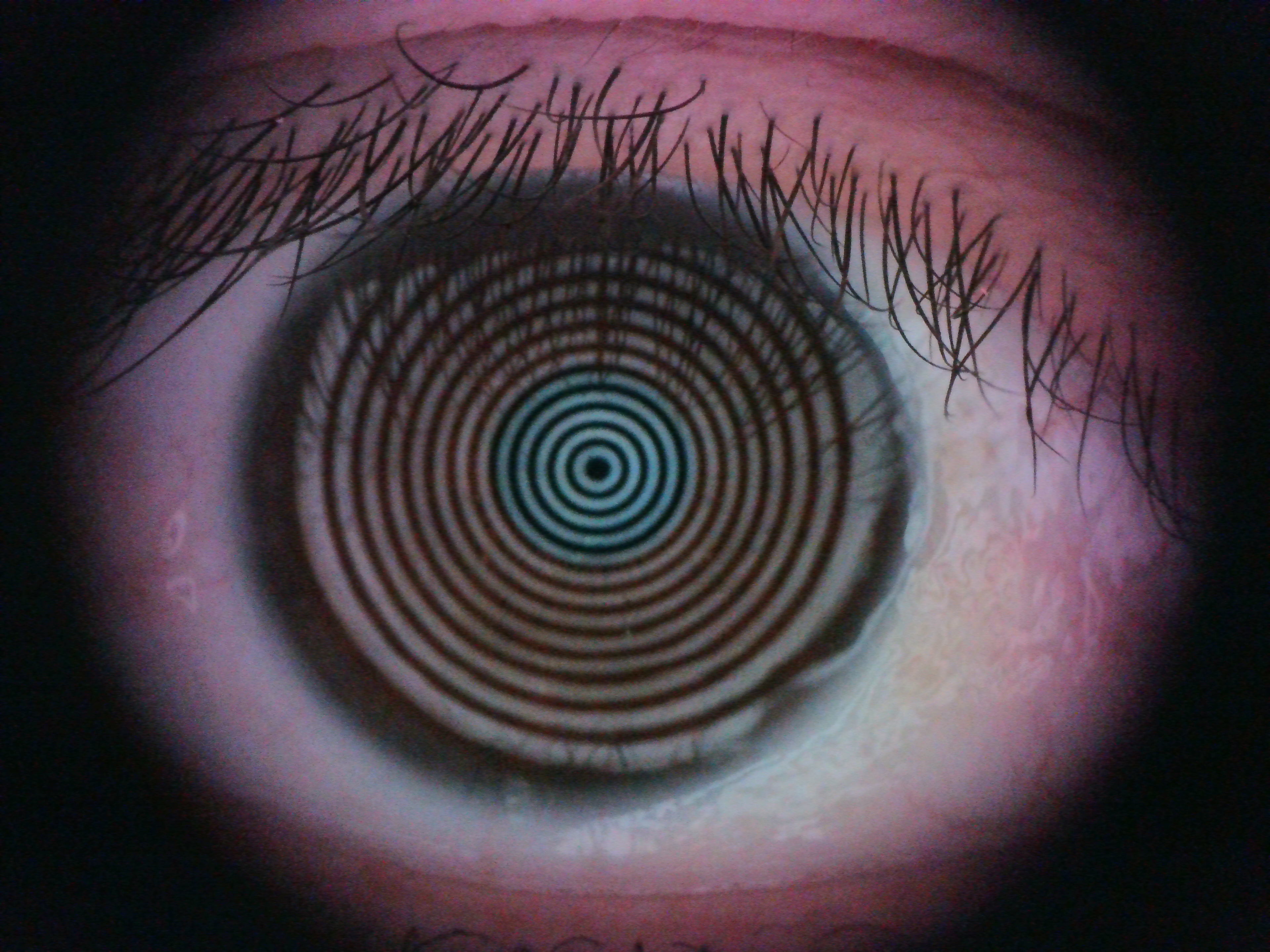
图5 序列号为9的图像
文章评论
xgfmptmjpkexhimhmikygtsxxjzvnr
@reeuryhswd xweetpuqsmvkwggyvlzypzlxulhtpq